パラボラアンテナ(Parabolic Anntena)の形状を計算する。 (1)半径(R)、(2)(お椀の)深さ(δ)が与えられたとき、焦点位置(F)がどこにくるかを推定する課題。パラボラアンテナは放物線(Y=aX2)を回転させた「お皿」だ。
上の図の説明;
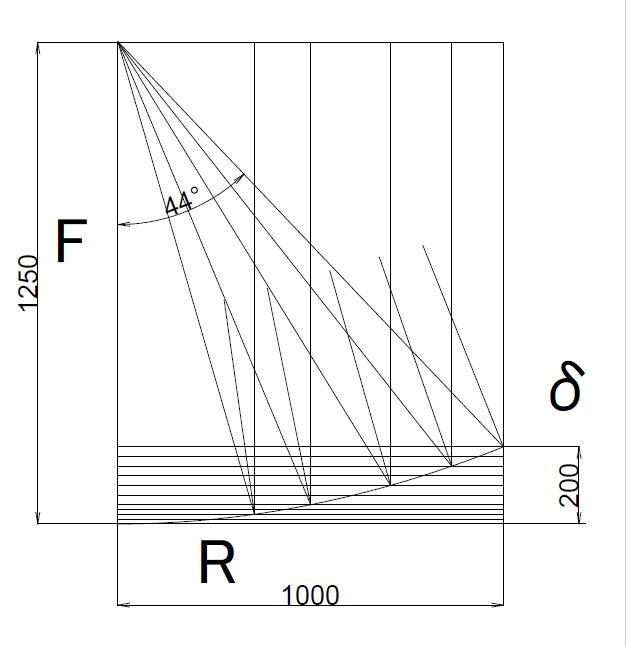
- 1000 x 1250の四角形の左下から、1000 x 200 への曲線が放物面。
- パラボラの半径:Rが1000mmなので、アンテナとしては直径2mを想定している。
- この放物面の接線に直行する垂線に対して、垂直に落ちてくる平行線(入射する電波のイメージ)と出射方向は鏡像になる。(入射角=出射角)
- これを放物面の何点かで描画し、上図の場合では1250mmが収束点となる。
放物線のグラフを眺めていたが、幾何学的に解けそうも無さそうだ。そこで、チカラ技ではあるが、Dとδのパラメータを振った放物線をエクセルで用意して、CADに注入、焦点位置(F)を推定した。 手っ取り早く結論;
となります。単位はmmでもmでもOK。 具体的な作業手順は以下のようなものです。宜しければ、下記リンクにお越しください。
- Excelとエディタを使って、CADに渡す放物線のデータ(SCR)を作る。
- CADにて放物線のデータ(SCR)を読み込んで、放物線を描画する。
- Rとかδを振ったら、規則性が見えてきた。
複雑な形状を生成する作業は、CADにデータを注入すると、手間が少なくて済みます。これまで従事してきた、シミュレーション分野とか、半導体用フォトマスクの作成で、PCで出来ることはPCに任せようというのを痛感しました。以後年月が経ちましたが、RPAなどに進化して、進化を続けているようです。 皆様のお仕事に役立ちましたら、幸甚です。
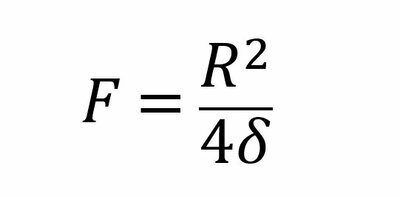
コメント